Dynamic PET imaging itinerary
In this post, I am summarizing some materials on dynamic PET imaging, especially the compartment model analysis.
Book chapters
- Physics in Nuclear Medicine, Simon R. Cherry et. al., Sanders, 2012 4th ed.
Chapter 21 of this book, “Tracer Kinetic Modeling”, briefly discusses the basic principles in kinetic analysis and the compartment modeling, and presented several models. It emphasizes on the transportation of the blood, and briefly deals with the FDG model. It is of an entry level (undergraduate level), not especially focusing on neurology. However, not too much information on the compartment model is presented. - Basic Sciences of Nuclear Medicine, edited by Magdy M. Khalil, Springer, 2011.
Chapter 16 of this book, “Tracer Kinetic Modeling: Basics and Concepts”, by Kjell Erlandsson from University College of London, concisely summarized several major concepts and models in kinetic modeling. It goes through the basic derivative equations that describe the behavior of the tracers in the compartments. Nicely written reference.
Chapter 17 of this book, “Tracer Kinetic Modeling: Methodology and Applications”, by M’hamed Bentourkia from Université de Sherbrooke, Canada, focuses on the practical aspects of dynamic PET and kinetic modeling studies. It also briefly introduced the spectral analysis. - Basic Science of PET Imaging, edited by Magdy M. Khalil, Springer, 2016.
This book is a daughter book to the one above. They are related, but quite different.
Chapter 14 of this book, “Compartmental Modeling in PET Kinetics”, by Hiroshi Watabe from Tohoku University, is rather practical for data analysis. It is written rather logically, touching some practical issues such as model fitting. So, it is brief and comprehensive.
Watabe worked under Richard Carson, and is still maintaining Carson’s BLD software by porting it in to python as pyBLD. - Emission Tomography: The Fundamentals of PET and SPECT, edited by Miles N. Wernick and John N. Aarsvold, Elsevier, 2004.
Chapter 23 of this book, “Kinetic Modeling in Positron Emission Tomography”, by E. D. Morris et. al.. - Positron Emission Tomography: Basic Sciences, edited by Dale L. Bailey et. al., Springer, 2005.
Chapter 6 of this book, “Tracer Kinetic Modeling in PET”, by Richard E. Carson. - Quantitative Analysis in Nuclear Medicine Imaging, edited by Habib Zaidi, Springer, 2006.
Chapter 12 of this book, “Tracer Kinetic Modeling in Nuclear Medicine: Theory and Applications”, by M. Bentourkia and H. Zaidi.
Review Articles
- Hooker, Jacob M., and Richard E. Carson. “Human positron emission tomography neuroimaging.” Annual Review of Biomedical Engineering 21 (2019): 551-581.
In this review article, the authors summarized comprehensively all aspects of neuroimaging. Part of it discusses modeling in a straightforward way, however, it is based entirely on the reference tissue method. - Watabe, Hiroshi, et al. “PET kinetic analysis—compartmental model.” Annals of Nuclear Medicine 20.9 (2006): 583-588.
This short review article connects various concepts in the compartment model analysis, and introduced several impressive examples. It is definitely well-written, but is somewhat brief.
Software
- KMtoolbox
KMToolbox is a MATLAB program to directly estimate various model parameters, directly measured from the 4D image. It is capable of processing both PET and DCE-MRI.
However, the major limitation is the lack of reliable documentations. Although the code is clearly written with ample comments, and the author Michele Scipioni provided some further information on the Project Page, there are still some confusing aspects, as the conventions and notations in kinetic modeling are not unified. - pmod
pmod is a commercial software built with JAVA, and is rather costly. I am not a big fan of pmod, but admittedly it provides some very useful application-specific shortcut solutions. The modules involved in kinetic modeling are PKIN (parameter estimation, etc.) and PXMOD (pixel/voxel-wise modeling). Admittedly, pmod integrates some kinetic models which save a lot of efforts.
Representative researchers
- Richard E. Carson
Carson is one of the pioneers in PET kinetic modeling. He earned his PhD in UCLA, and he should have got some relationships with Michael Phelps or Edward Hoffman. Now he is leading a team in Yale. - Yun Zhou
Now in United Imaging Healthcare, Dr. Zhou is known for developing the reverse equilibrium plot and multi-graphical analysis. - Richard Wahl
Richard Wahl is one of the leading PET researchers in the US, and is the head of the radiology department of WUSTL. He is also one of the leading researchers in dynamic PET. - Guobao Wang
Guobao Wang is in UCDavis and his recent research highlight is on EXPLORER PET. He has a code for direct reconstruction of dynamic PET, DIRECT v0.1.
Notes
Graphical analysis
In graphical analysis, $C(t)$ is the concentration of the tracer in the ROI, $C_P(t)$ is the concentration in plasma.
- Patlak plot, or Gjedde-Patlak plot
Here, $K_i$ is obtained by regression. Patlak model assumes non-reversible uptake.
- Logan plot
Here, $DV_\mathrm{L}$ correspond to the distribution volume. Logan also applies to reversible tracers.
- Reverse equilibrium (RE) plot
RE is another version of Logan.
Compartment Models
Here, $C_\mathrm{P}$ means the plasma concentration, $C_\mathrm{F}$ corresponds to the free tracer in tissue, $C_\mathrm{S}$ corresponds to the specific binding, and $C_\mathrm{NS}$ corresponds to the non-specific binding.
$C_\mathrm{ND}$ is the non-displacable tracer concentration, and \(C_\mathrm{ND} = C_\mathrm{F} + C_\mathrm{NS}\) while $C_\mathrm{T}$ is the total concentration of the tissue, and \(C_\mathrm{T} = C_\mathrm{S} + C_\mathrm{ND}\)
The rate constant $K_1$ is capitalized because it is usually in a different unit.
- 1TC
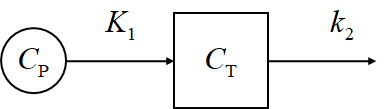
Kinetic equation
\[\frac{\mathrm{d}C_\mathrm{T}}{\mathrm{d}t} = K_1 C_P - k_2 C_\mathrm{T}\]Solution
\[C_\mathrm{T}(t) = K_1 \mathrm{e}^{-k_2t}*C_\mathrm{P}(t)\]- 2TC
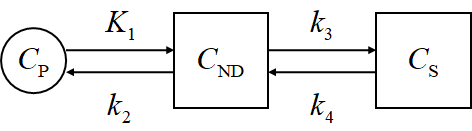
- 3TC
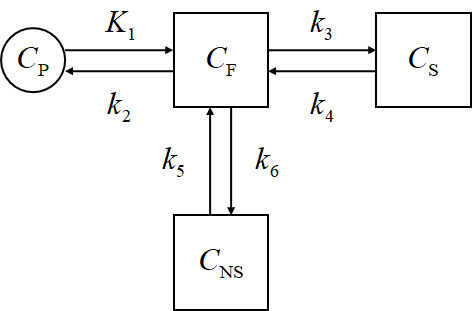
- Reference tissue method
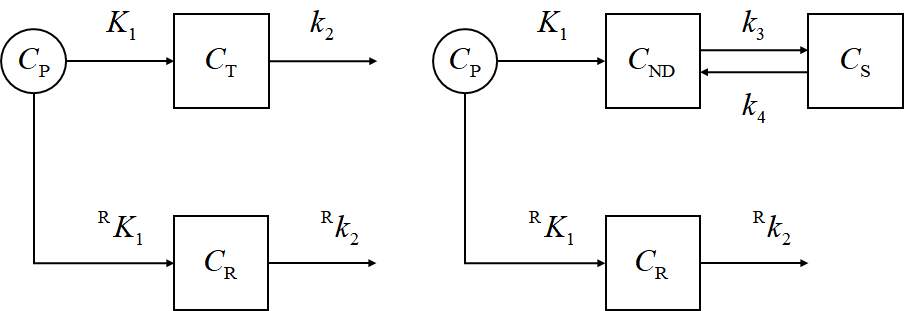
Important concepts
- Binding potential ($BP$)
The ratio between the bound radioligand to the unbound radioligand. An in vitro definition could be
\[BP \equiv \frac{B_\mathrm{max}}{K_D}\]Alternatively, several other types of $BP$ can be defined:
\[\begin{array}{rcl} BP_\mathrm{F} & \equiv & \left[\frac{C_\mathrm{S}}{C_\mathrm{P,F}}\right]_\mathrm{eq} \\ BP_\mathrm{P} & \equiv & \left[\frac{C_\mathrm{S}}{C_\mathrm{P}}\right]_\mathrm{eq} \\ BP_\mathrm{ND} & \equiv & \left[\frac{C_\mathrm{S}}{C_\mathrm{ND}}\right]_\mathrm{eq} \end{array}\]$C_\mathrm{P,F}$ is the free tracers in the plasma,
\[C_\mathrm{P,F} \equiv f_\mathrm{P}C_\mathrm{P} = C_\mathrm{F} \equiv f_\mathrm{ND}C_\mathrm{ND}\]where $f_\star$ is the free fraction.
- Distribution volume ($V_T$, or $DV$)
The notations are defined later.
-
Partition coefficient ($\lambda$)
-
Summary of the relationships
| Name | Definition | 3TC | 2TC | DV |
|---|---|---|---|---|
| $BP_\mathrm{F}$ | $\frac{B_\mathrm{avail}}{K_D}$ | $\frac{k_3}{k_4}$ | $\frac{1}{f_\mathrm{P}}\frac{K_1k_3}{k_2k_4}$ | $\frac{1}{f_\mathrm{P}}(V_T - V_\mathrm{ND})$ |
| $BP_\mathrm{P}$ | $f_\mathrm{P}\frac{B_\mathrm{avail}}{K_D}$ | $\frac{k_3}{k_4}$ | $\frac{K_1k_3}{k_2k_4}$ | $V_T - V_\mathrm{ND}$ |
| $BP_\mathrm{ND}$ | $f_\mathrm{ND}\frac{B_\mathrm{avail}}{K_D}$ | $\frac{k_3}{k_4}\frac{k_6}{k_5+k_6}$ | $\frac{k_3}{k_4}$ | $\frac{V_T-V_\mathrm{ND}}{V_\mathrm{ND}}$ |
| $V_T$ | $\left[\frac{C_\mathrm{T}}{C_\mathrm{P}}\right]_\mathrm{eq}$ | $\frac{K_1}{k_2}(1+\frac{k_3}{k_4}+\frac{k_5}{k_6})$ | $\frac{K_1}{k_2}(1+\frac{k_3}{k_4})$ | - |
Milestone publications
Representative tracers
- [$^{18}$F]FDG
- Sommariva, Sara, et al. “Mathematical Models for FDG Kinetics in Cancer: A Review.” Metabolites 11.8 (2021): 519.
A lengthy review on the development of FDG models. - Hays, Marguerite T., and George M. Segall. “A mathematical model for the distribution of fluorodeoxyglucose in humans.” Journal of Nuclear Medicine 40.8 (1999): 1358-1366.
Evaluate the whole body kinetics of FDG in human.
- Sommariva, Sara, et al. “Mathematical Models for FDG Kinetics in Cancer: A Review.” Metabolites 11.8 (2021): 519.
- [$^{11}$C]PiB
The Turku PET center page summarizes many related researches, for example,- Chen, Yin Jie, and Ilya M. Nasrallah. “Brain amyloid PET interpretation approaches: from visual assessment in the clinic to quantitative pharmacokinetic modeling.” Clinical and Translational Imaging 5.6 (2017): 561-573.
This paper uses the reference tissue method.
- Chen, Yin Jie, and Ilya M. Nasrallah. “Brain amyloid PET interpretation approaches: from visual assessment in the clinic to quantitative pharmacokinetic modeling.” Clinical and Translational Imaging 5.6 (2017): 561-573.
- [$^{99m}$Tc]Tc-MDP
MDP is a SPECT tracer, but due to the extreme importance and widespread applications, the kinetic study attracts much attention.- Schroth, Hans-Joachim, et al. “Comparison of the kinetics of methylene-diphosphonate (MDP) and dicarboxypropan-diphosphonic acid (DPD), two radio-diagnostics for bone scintigraphy.” European Journal of Nuclear Medicine 9.12 (1984): 529-532.
Note
- Use MLA-style citations.